Leibniz-Objekt des Monats
August 2016: Der Leibniz'sche Analogrechner
Der Leibniz’sche Analogrechner
Das Leibniz-Objekt des Monats Mai hat den Nachbau der Leibnizʼschen Vier-Spezies-Rechenmaschine vorgestellt. Diese Maschine, die dreizehn anderen Nachbauten und die vier Originalmodelle, die Gottfried Wilhelm Leibniz zu Lebzeiten anfertigen ließ, sind dem Feld der digitalen Rechentechnik zuzuordnen, zu dem auch der Computer gehört. Daneben hat Leibniz auch Beiträge zur analogen Rechenkunst geleistet, die bis weit ins 20. Jahrhundert florierte.
So kennen ältere Leserinnen und Leser sicher noch den Rechenstab oder Rechenschieber, bestehend aus dem sogenannten Körper, der darin verschiebbaren Zunge und dem hin- und herfahrenden Läufer aus durchsichtigem Material. Das Instrument dient meist zur schnellen Multiplikation und Division und ist trotz der eingravierten Ziffern kein digitales Instrument, sondern arbeitet analog. Der Benutzer überträgt Zahlen auf korrespondierende Größen in der realen Welt, in diesem Fall auf Abschnitte auf den logarithmisch unterteilten Skalen des Stabes. Die Abschnitte setzt er aneinander oder zieht sie voneinander ab. Beim Ablesen der daraus resultierenden Strecke überträgt er wieder eine real existierende Größe in das Reich der Zahlen.
Der Rechenstab-Historiker Werner Rudowski wies 2007 darauf hin, dass sichLeibniz in seinen letzten Lebensjahren mit einem mathematisch dem Rechenstab verwandten Gerät befasste. Zwischen 1712 und 1715 stand er in regem Briefwechsel mit dem Markscheider und Ingenieur Bernhard Ripking (1682-1719) in Clausthal im Harz. In einem Schreiben vom 29. Mai 1712 erwähnte Leibniz „Auftragung von Logarithmorum auff Linien, damit man zimliche Zahlen leicht multiplizieren und divieren kann“. Er bat Ripking um das Anfertigen eines Zylinders und das Auftragen einer logarithmisch unterteilten Schraubenlinie auf dem Zylindermantel. Die Linie, das sei ergänzt, würde sich mehrmals um den Zylinder winden und entspräche der Skala eines Rechenstabs. Zum Rechnen müsste man mit einem Zeiger Punkte auf der Linie bzw. ihren Abstand abgreifen.
In seiner umgehenden Antwort vom 3. Juni 1712 äußerte Ripking Zweifel an der Realisierung des Konzepts und schlug stattdessen eine Rechenscheibe mit zwei gegeneinander verschiebbaren Skalen vor. Leibniz reagierte seinerseits prompt und schilderte in seinem Schreiben vom 20. Juni 1712 einen Weg zur Rettung seiner ursprünglichen Idee: Man könne die logarithmische Skala in einen Metallfaden ritzen, diesen entlang einer auf dem Zylinder gravierten Schraubenlinie aufwickeln und die Skala übertragen. Damit endete die Korrespondenz der beiden Herren zur Analogtechnik. Nachzutragen bleibt, dass sowohl die Ripking’sche Rechenscheibe als auch der Leibniz’sche Rechenzylinder im 19. Jahrhundert kommerziell hergestellt und vermarktet wurden.
Der Leibniz’sche Constructor
Die Weiterentwicklung des Rechenstabs ist der Analogrechner. Er verbreitete sich im 19. Jahrhundert und trat zunächst in mechanischer Form und speziellen Typen auf, wie Planimeter, Integraph, Gezeitenrechner oder Differentialanalysator. Nach dem Zweiten Weltkrieg entstanden flexibel einsetzbare elektrische Modelle, die bis in die 1970er Jahre in Gebrauch waren. Sie enthielten zunächst Elektronenröhren und später Transistoren, und sie ließen sich durch Einstecken von Kabeln und Einstellen von Drehschaltern programmieren. Bereits dreihundert Jahre zuvor hatte Leibniz das Konzept eines spezialisierten mechanischen Analogrechners – vermutlich der erste in der Geschichte der Mathematik – in zwei Manuskripten vom Dezember 1674 beschrieben, d.h. in seiner Pariser Zeit.
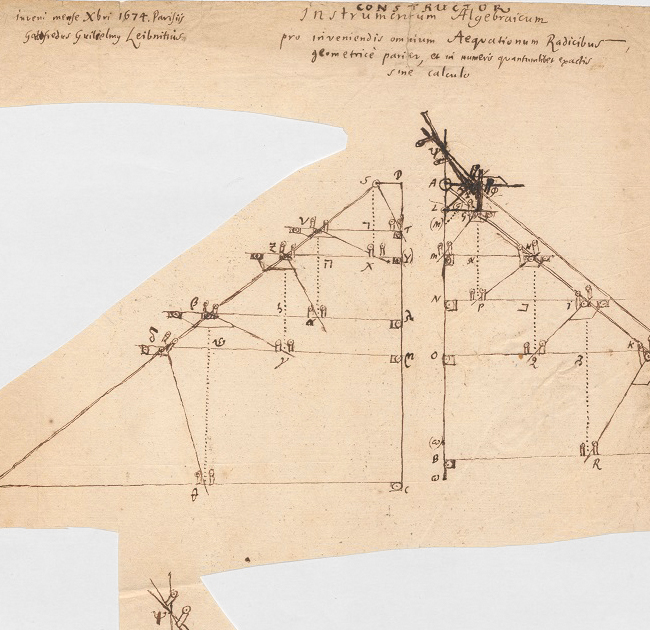
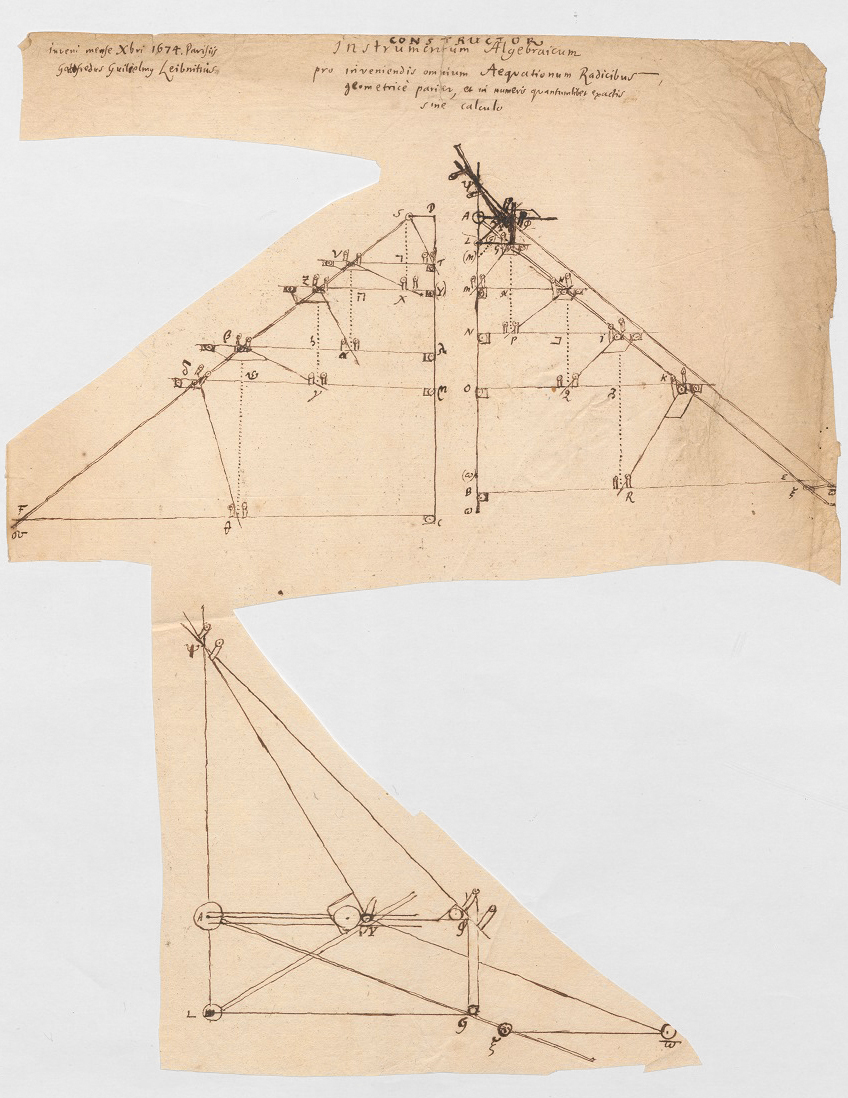
Erstmalig ausgeführt hat Leibniz seine Idee in der immerhin neunseitigen Handschrift „Constructor. Instrumentum Algebraicum pro inveniendis omnium Aeqvationum Radicibus, geometricè pariter, et in numero qvantumlibet exactis sine calculo“. Weiterverfolgt hat er den Gedanken schließlich in der zwölfseitigen Gedankenskizze „Schediasma de constructore“.
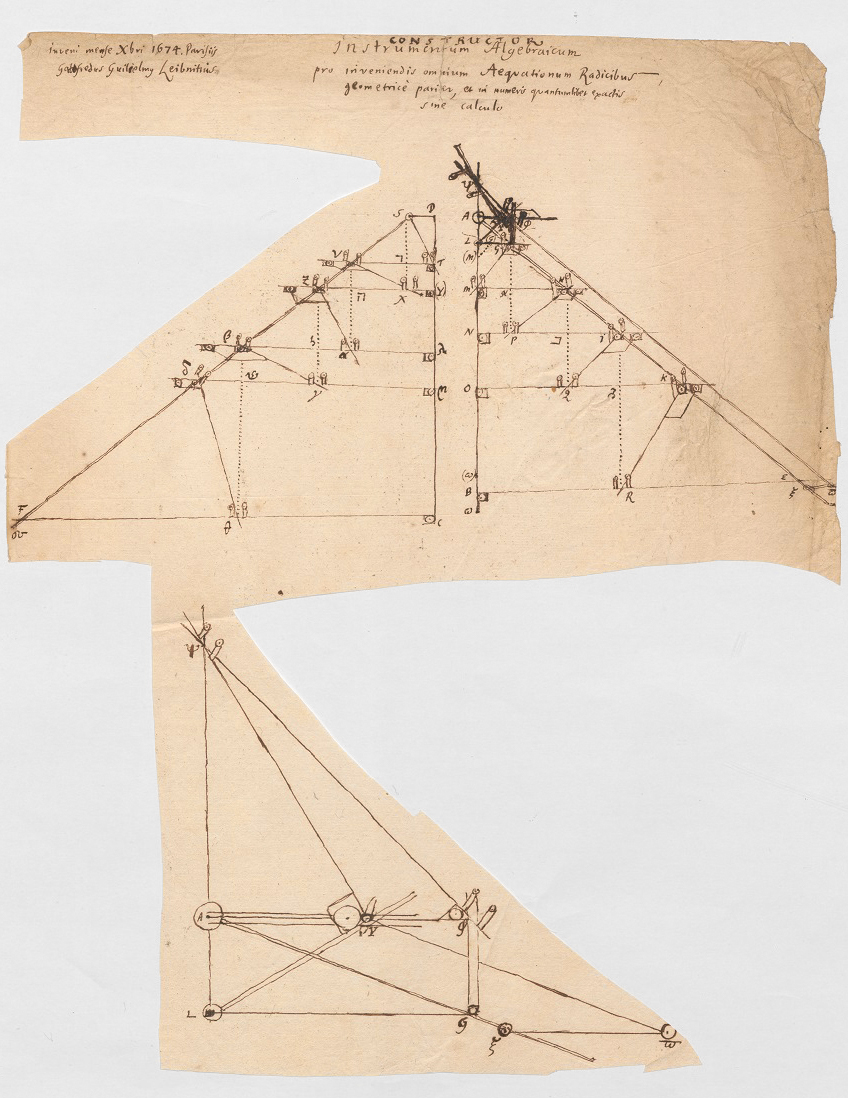
Abbildung: Leibnizʼ „Constructor. Instrumentum Algebraicum pro inveniendis omnium Aeqvationum Radicibus, geometricè pariter, et in numero qvantumlibet exactis sine calculo“, 9. Seite, © GWLB Hannover, LHXXXV, III A 20, 5v.
Der Leibniz’sche Constructor besteht aus Stangen, Schnüren, Rollen und Gelenken und hat den Zweck, Lösungen einer algebraischen Gleichung zu finden. Es soll also beispielsweise das x aus ax + bx² + cx³ = d ermitteln. Dafür stellt man zunächst am Gerät die Werte für a, b und c sowie einen beliebigen Startwert x1 für x ein. Diese Einstellungen verändern das Gestänge und bewirken, dass man am Constructor eine Strecke der Länge ax1 + bx1² + cx1³ ablesen kann. Diese ist vermutlich noch nicht gleich d. Durch weiteres Verschieben und Verdrehen von Stangen lässt sich die variable Größe x aber so ändern, dass ax + bx² + cx³ im Rahmen der Genauigkeit gleich d wird, womit das Ziel erreicht wäre.

Abbildung: Leibnizʼ „Constructor. Instrumentum Algebraicum pro inveniendis omnium Aeqvationum Radicibus, geometricè pariter, et in numero qvantumlibet exactis sine calculo“, 1. Seite, © GWLB Hannover, LHXXXV, III A 20, 1r.
Die Beschreibung hier gibt die Komplexität der Leibniz’schen Konstruktion nur unvollkommen wieder, und für Details verweisen wir den Leser auf den 1970 veröffentlichten Aufsatz des Mathematikhistorikers Joseph Ehrenfried Hofmann (1900-1973). Die mathematische Basis des Constructors ist der seit der Antike bekannte Strahlensatz, und die Anzeige beschränkt sich auf reelle Lösungen der Gleichung. Wie die Skizzen von Leibniz andeuten, sollte der Rechner aus zwei ähnlich aufgebauten Segmenten bestehen. Das eine bearbeitet den Gleichungsteil mit positiven Koeffizienten, das andere den Teil mit negativen Koeffizienten.
Die zweite Erfindung des Constructors
Der von Leibniz erdachte Analogrechner verschwand in den Akten, ein Rechner ähnlichen Prinzips wurde jedoch 42 Jahre nach Leibnizʼ Tod, sehr wahrscheinlich unabhängig von diesem, erneut erfunden und zehn Jahre später in ein funktionsfähiges Modell umgesetzt, und zwar durch Johann Andreas von Segner (1704-1777), der seit 1732 Mathematik und Naturwissenschaften in Jena, Göttingen und Halle lehrte. 1758 ersann Segner ein geometrisches Verfahren zum Lösen einer algebraischen Gleichung, das 1761 unter dem Titel „Methodus simplex et universalis, omnes omnium aequationum radices detegendi“ im Jahrbuch der kaiserlich-russischen Akademie der Wissenschaften. „Novi Commentarii Academiae Scientiarum Imperialis Petropolitanae“ erschien (VII, S. 211-226).
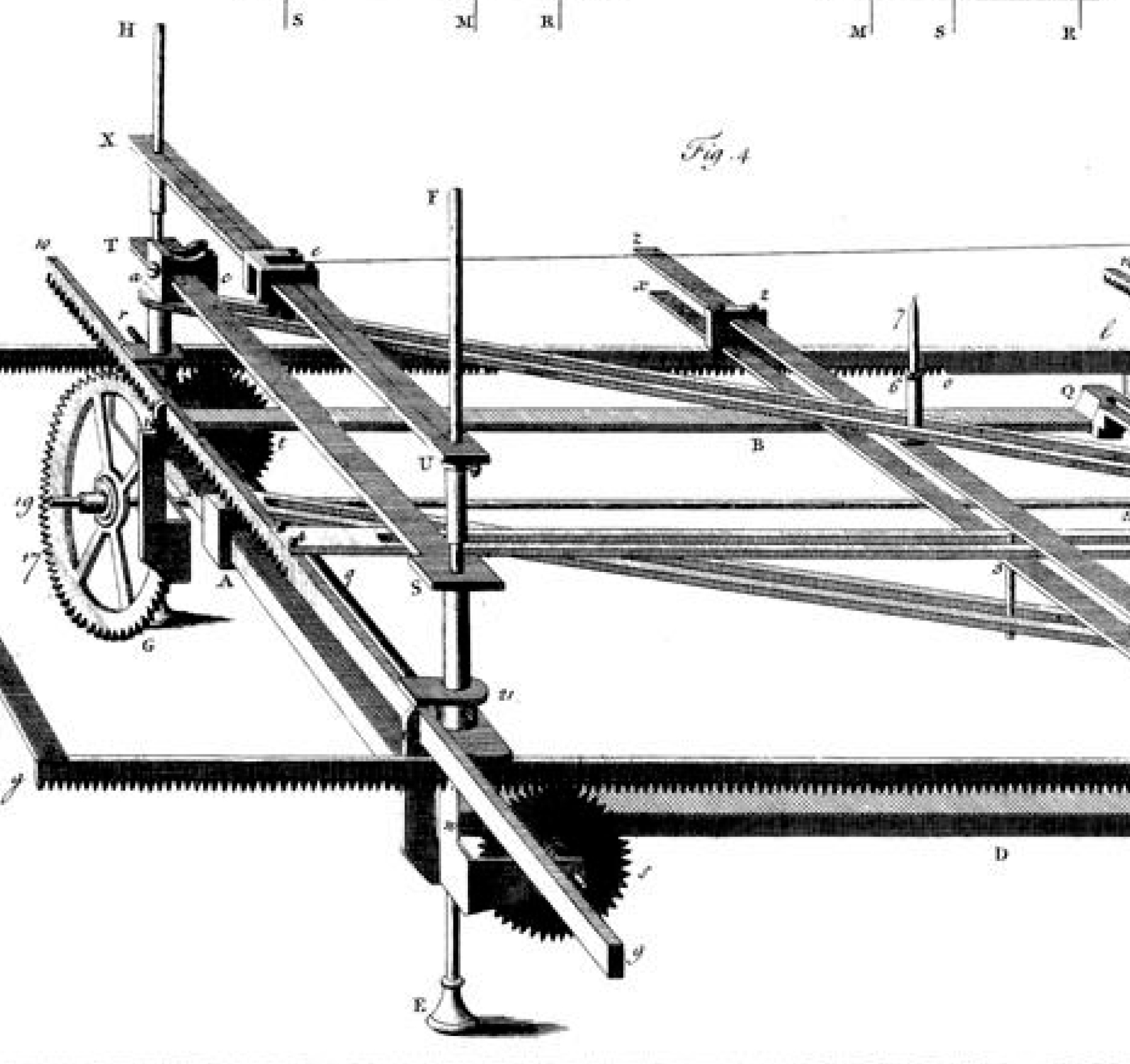
Segners Arbeit stellt ein abstraktes Rechengerät dar, in das man, um bei obigem Beispiel zu bleiben, die Koeffizienten a, b, c und d sowie einen Wert für x eingibt und die Summe ax + bx² + cx³ - d erhält. Sein Gerät war einfacher als das von Leibniz, da es den Strahlensatz auf geschicktere Weise nutzte. Auf dieser Grundlage konnte der Engländer John Rowning der Londoner Royal Society 1768 ein funktionsfähiges Modell vorlegen. Zwei Jahre später erschien auf den Seiten 240 bis 256 von Band LX (1770) der „Philosophical Transactions” der Society Rownings Aufsatz „Directions for making a Machine for finding the Roots of Equations universally, with the Manner of using it”.
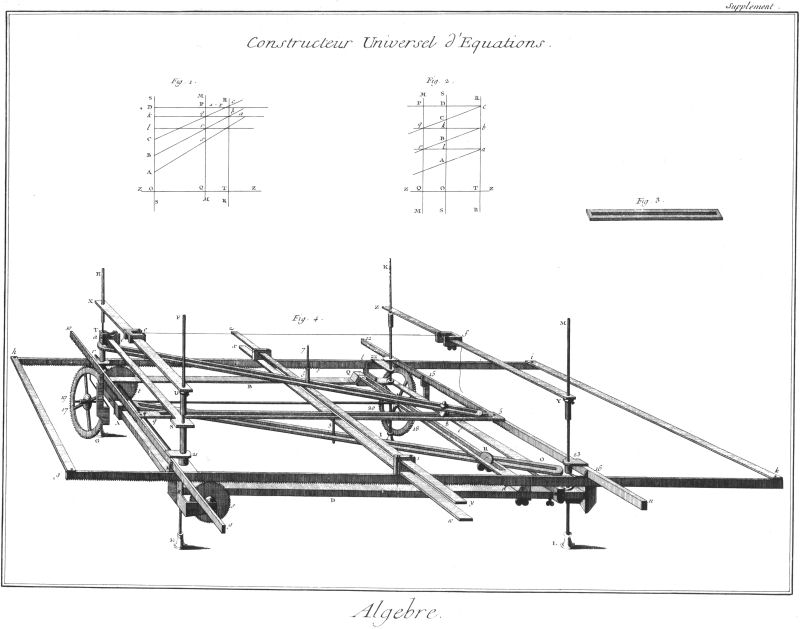
Abbildung: Darstellung des Instruments von John Rowning im Tafelband des „Supplément à l'encyclopédie ou dictionaire raisonné des sciences des Arts et des métiers“ (Amsterdam 1776) zum Artikel „Équation, Construction & usage d'une machine pour trouver les racines de quelque équation que ce puisse être“.
Damit ist die Geschichte des Constuctors aber keineswegs zu Ende, denn in den 1990er Jahren entstanden in Italien zwei weitere Realisierungen des Leibniz-Segner-Rowning-Rechners. Verantwortlich waren die Forscher Franco Conti und Aldo Frediani, die Exponate für eine Mathematikausstellung suchten. Sie erhielten 1995 das italienische Patent ITFI940083 für eine „Macchina generatrice di polinomi“ (Maschine zur Erzeugung von Polynomen). Damit wurde der Leibniz’sche Geistesblitz von 1674 gesetzlich geschützt – zumindest temporär, denn das Patent dürfte inzwischen abgelaufen sein.
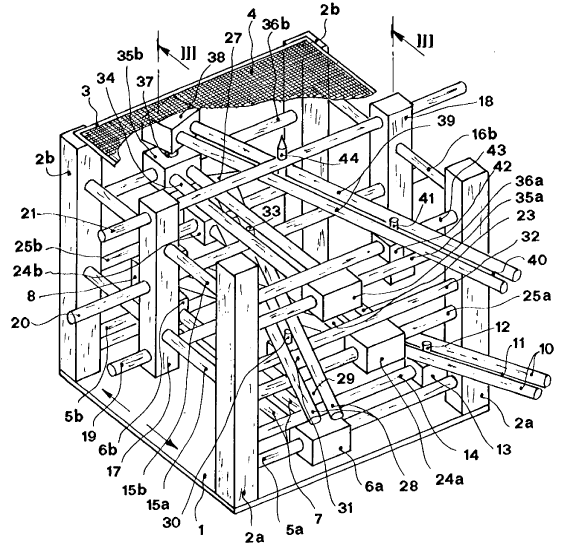
Abbildung: Zeichnung der Maschine von Franco Conti und Aldo Frediani aus dem italienischen Patent © ITFI940083.
Autor: Ralf Bülow, freiberuflicher Wissenschafts- und Technikhistoriker in Berlin
Literaturhinweise:
Die Handschriften des Briefwechsels zwischen Leibniz und Ripking finden sich in der Niedersächsischen Staats- und Universitätsbibliothek Göttingen (SUB Göttingen, 8 Cod. Ms. philos. Bl. 1-5) bzw. im Niedersächsischen Landesarchiv – Hauptstaatsarchiv Hannover (Cal. Br. 4 Nr. 114).
Stefan Drechsler, Barbara Häberlin, „Eine geometrische Wurzelbehandlung – Von der Idee zur Maschine durch fünf Sprachen, fünf Nationen und drei Jahrhunderte“ (2006), abrufbar unter http://www.rechnerlexikon.de/files/rowning.pdf
Josef Ehrenfried Hofmann, "Über frühe mathematische Studien von G. W. Leibniz", in: Studia Leibnitiana 2 (2), 81 - 114.
Werner H. Rudowski, „Leibniz und sein logarithmischer Rechenzylinder“ (2007), abrufbar unter http://www.rechenschieber.org/Leibniz.pdf
Heinz Nixdorf MuseumsForum, „Herr Leibniz und sein Analogrechner“ (2016), abrufbar unter http://blog.hnf.de/herr-leibniz-und-sein-analogrechner/