Leibniz-Objekt des Monats
Juli 2016: Leibniz und die "Baroulkos-Maschine"
Leibniz und die „Baroulkos-Maschine“. Ein kleines Rätsel aus dem Bereich der Quellenforschung
Als Leibniz 1672-1676 in Paris weilte, widmete er sich Galileis Abhandlung Discorsi e dimostrazioni matematiche (1638). Bei der Lektüre wurde er unter anderem auf das mechanische Phänomen der Reibung aufmerksam, insbesondere auf die Verzögerung, die den Körpern widerfährt, wenn sie sich in einem widerstehenden Medium bewegen. Vom Thema angeregt, nahm sich Leibniz vor, eine mathematische Beschreibung des Phänomens zu liefern. Damit wollte er nicht nur einen Beitrag zur wissenschaftlichen Bewegungslehre leisten, sondern auch praktische Ziele erreichen: Durch die Verbesserung der Leistungen von Maschinen wollte er indirekt menschlichen Unterfangen zum Erfolg verhelfen. In Pariser Handschriften aus dem Jahr 1675, die jetzt im Band VIII.2 der Leibniz-Edition veröffentlicht werden, beklagt er sich darüber, dass keine seiner Vorgänger sich um eine Berechnung der Reibung bemüht hatten:
„Die Geometer haben über diesen Gegenstand noch keine Regeln geliefert, und diejenigen, die Abhandlungen über die Mechanik verfasst haben, erwähnen ihn nur nebenbei und mit der Absicht, ihn erfahrenen Handwerkern zu überlassen. Es steht dennoch fest, dass gut durchdachte Vorhaben oftmals gescheitert sind, weil ein großer Teil der bewegenden Kraft vernichtet worden war, um die Reibung unter den Bestandteilen der Maschine zu überwinden. Davon betroffen sind bekanntlich die Maschinen zum Hochheben großer Lasten, die Pumpen, die Karren und weitere Fuhrwerke, und man hat neue Mittel gesucht – und bald auch gefunden –, um den Kraftverlust zu meiden.“ (Du frottement. Essais géometriques en fait de mechanique, in LSB VIII.1, N.~36)
 Abbildung 1: Hannover, Gottfried-Wilhelm-Leibniz-Bibliothek, LH XXXV 9, 11 Bl.~3r. (Detail).
Abbildung 1: Hannover, Gottfried-Wilhelm-Leibniz-Bibliothek, LH XXXV 9, 11 Bl.~3r. (Detail).
Leibniz zufolge ist es also nicht nur wünschenswert, sondern auch möglich, Maschinen zu bauen, bei denen die Reibung minimiert wird. Als Beispiel erwähnt er eine Maschine von Claude Perrault, einem der vielen Intellektuellen, mit denen er in Paris verkehrte: „Monsieur Perrault hat in seinem Vitruvius eine Maschinenart zum Hochheben von Lasten, oder Barulcum, bekanntgemacht, in welcher die Reibung kaum vorkommt.“ (ebd.)
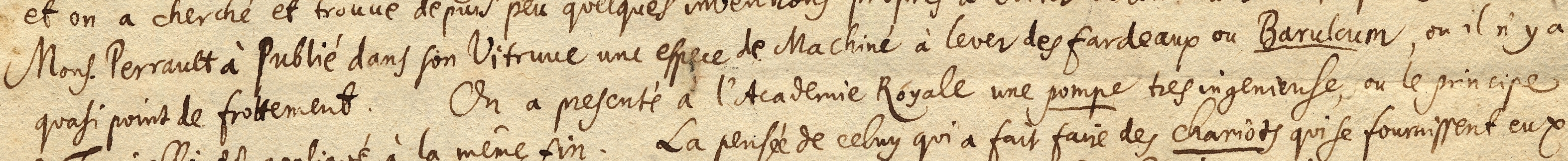 Abbildung 2: Hannover, Gottfried-Wilhelm-Leibniz-Bibliothek, LH XXXV 9, 11 Bl.~3r. (Detail).
Abbildung 2: Hannover, Gottfried-Wilhelm-Leibniz-Bibliothek, LH XXXV 9, 11 Bl.~3r. (Detail).
Claude Perrault (1613-1688) – Arzt, Naturphilosoph, Humanist und Architekt – war mit dem monumentalen Umbau des Louvre beauftragt, als Leibniz sich in Paris aufhielt. Die Erfindung hocheffizienter Maschinen war für Perrault also kein Zeitvertreib, sondern ein Geschäft von unmittelbarem Interesse. In seiner Erwähnung bezieht sich Leibniz jedoch auf eine Erfindung, von der wir nicht wissen, ob sie auf der Louvre-Baustelle verwendet wurde. Perrault beschreibt sie „in seinem Vitruvius“, d.h. in seiner kommentierten französischen Übersetzung der Abhandlung über die Baukunst (De architectura), die auf den römischen Baumeister Vitruvius (1.Jh.v.Chr.) zurückgeht. In den Kommentaren zum zehnten Buch der Abhandlung, in dem Vitruvius Maschinen beschreibt, die in der Baukunst und der Kriegsführung Anwendung fanden, schildert Perrault tatsächlich – nicht ohne Stolz – einen von ihm entworfenen Kran, mit dessen Hilfe große Gewichte bei niedriger Reibung und verringertem Kraftverlust hochzuheben seien. Die besondere Leistung dieses Krans rührt Perrault zufolge von der Verwendung eines Rades zur Übertragung der hebenden Kraft her, wie in der folgenden Abbildung zu erahnen ist.
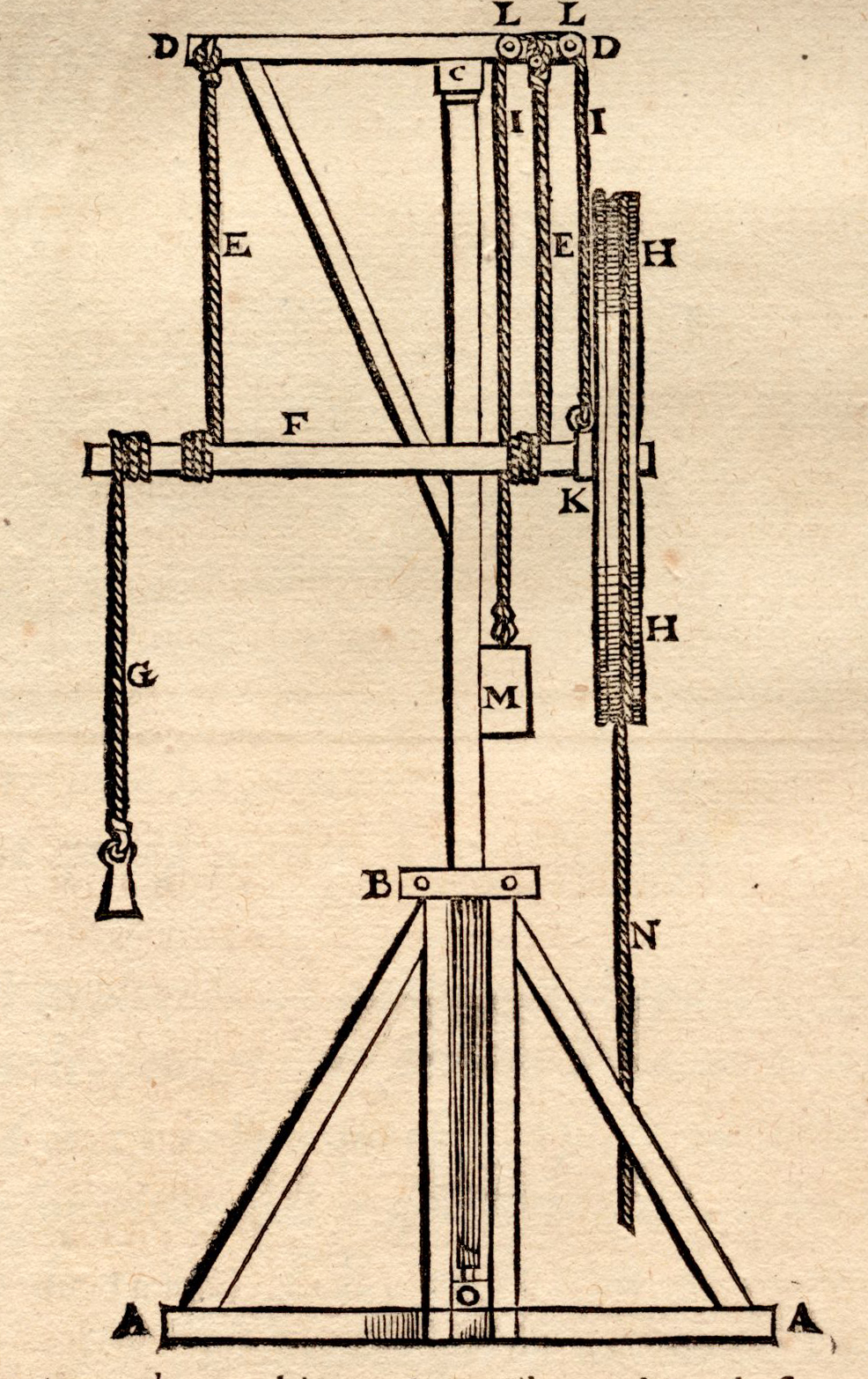
Abbildung 3: Vitruvius, Les dix livres dʼarchitecture, Paris 1673, S.280 (Detail), Stiftung Bibliothek Werner Oechslin.
Es dürfte somit kein Zweifel bestehen, dass dies die Maschine ist, auf die sich Leibniz in seiner Anspielung bezieht. Merkwürdig ist nur, dass Perrault sie weder barulcum nennt noch auf eine Maschine dieses Namens verweist. Leibniz scheint sich also geirrt zu haben. Es wäre auch kein Einzelfall in seinem gewaltigen Schriftenkorpus. Aber warum spricht er gerade von einem barulcum? Woher stammt der Begriff und wie kommt Leibniz darauf?
Vitruvius-Leser könnten nun denken, dass Leibniz in seiner Erwähnung nur ein kleiner Zuschreibungsfehler unterlaufen ist. Nicht Perraults Kran heißt barulcum, wohl aber eine Maschine, die Vitruvius selbst beschreibt, wie in modernen Textausgaben zu lesen ist: „Die dritte [Gattung der Maschinen] dient zum Ziehen; die Griechen nennen sie freilich baroulkos (βαρουλκός).“ (De architectura X, I, 1) Ihre Funktion ist der von Perraults Kran auch durchaus ähnlich, nämlich: schwere Gewichte zu heben und abzusetzen. (ebd. X, I, 2) Leibniz wird wohl also nur eine kleine Verwechselung unterlaufen sein. Welch ein Wunder, wenn man so viel – und so schnell – schreibt!
Die Lösung des Rätsels ist leider nicht so leicht, wie unsere Vitruvius-Kenner eventuell vermuten könnten. Denn die Lesart baroulkos kommt weder in Perraults Übersetzung noch überhaupt in der handschriftlichen Überlieferung von De architectura vor, sondern beruht auf einer Konjektur moderner Vitruvius-Editoren; die ältesten Handschriften überliefern stattdessen die Lesart baruison. Perrault selbst übernimmt eine weitere, von von frühneuzeitlichen Kommentatoren unterstützte Variante und übersetzt die soeben zitierte Stelle aus De architectura X, I, 1 folgendermaßen: „Le troisième [genre de machines] est pour tirer, quʼils [= les Grecs] appellent Banauson.“ (Les dix livres dʼarchitecture, S.~272A) Leibniz konnte also weder bei Perrault noch in Originalausgaben seiner Zeit eine Erwähnung der „Baroulkos-Maschine“ dort finden, wo heutige Vitruvius-Leser sie erwarten würden. Wo aber sonst? Und wie kommt es, dass Leibniz trotz seiner falschen Assoziation doch nicht ganz falsch lag? Das Rätsel wird dunkler. Es ist nun an der Zeit, etwas mehr über die historische Maschine zu sagen, die Vitruvius zufolge – wenn die modernen Editoren recht behalten – von den Griechen baroulkos genannt wurde.
Die Überlieferung dieser Maschine hängt wesentlich mit dem späthellenistischen Mathematiker und Ingenieur Heron von Alexandria (1.Jh.n.Chr.) zusammen, obwohl die antiken Quellen deren Erfindung keinem geringeren Naturforscher als Archimedes (um 287-212 v.Chr.) zuschreiben. Heron hat sie aber zu Beginn seiner Abhandlung „Mechanica“ ausführlich beschrieben. Diese Abhandlung wird in den Quellen sogar metonymisch als „Baroulkos“ bezeichnet, während die Maschine selbst weder bei Heron noch in der späteren Überlieferung eine eigene Benennung erhält. Streng genommen, ist es also falsch, baroulkos als Bezeichnung für eine spezielle Maschine zu betrachten. Vielmehr ging es dabei, wie auch Vitruviusʼ Formulierungen nahelegen, um eine Gattung von Maschinen, nämlich diejenige, die Heron in seinem Buch behandelt hatte. Aus Einfachheitsgründen soll im Folgenden aber weiterhin von einer „Baroulkos-Maschine“ die Rede sein.
Nach Herons Beschreibung war diese Maschine eine Hebewinde, d.h. tatsächlich ein Instrument, um (etwa bei Bauarbeiten) schwere Körper bei verringerter Kraftanwendung hochzuheben – ähnlich wie der von Perrault entwickelte Kran, auf den Leibniz in seinen Handschriften unter der Bezeichnung Barulcum verweist. Ihre Leistung rührte von der Aneinanderreihung wohlproportionierter Zahnräder her, die dazu dienen sollten, die Drehungen einer Kurbel zu übertragen – eine Anwendung, auf die Leibniz selbst in seinen technischen Entwürfen zuweilen rekurriert. Die Darstellung eines kleinformatigen Modells kann man hier sehen:
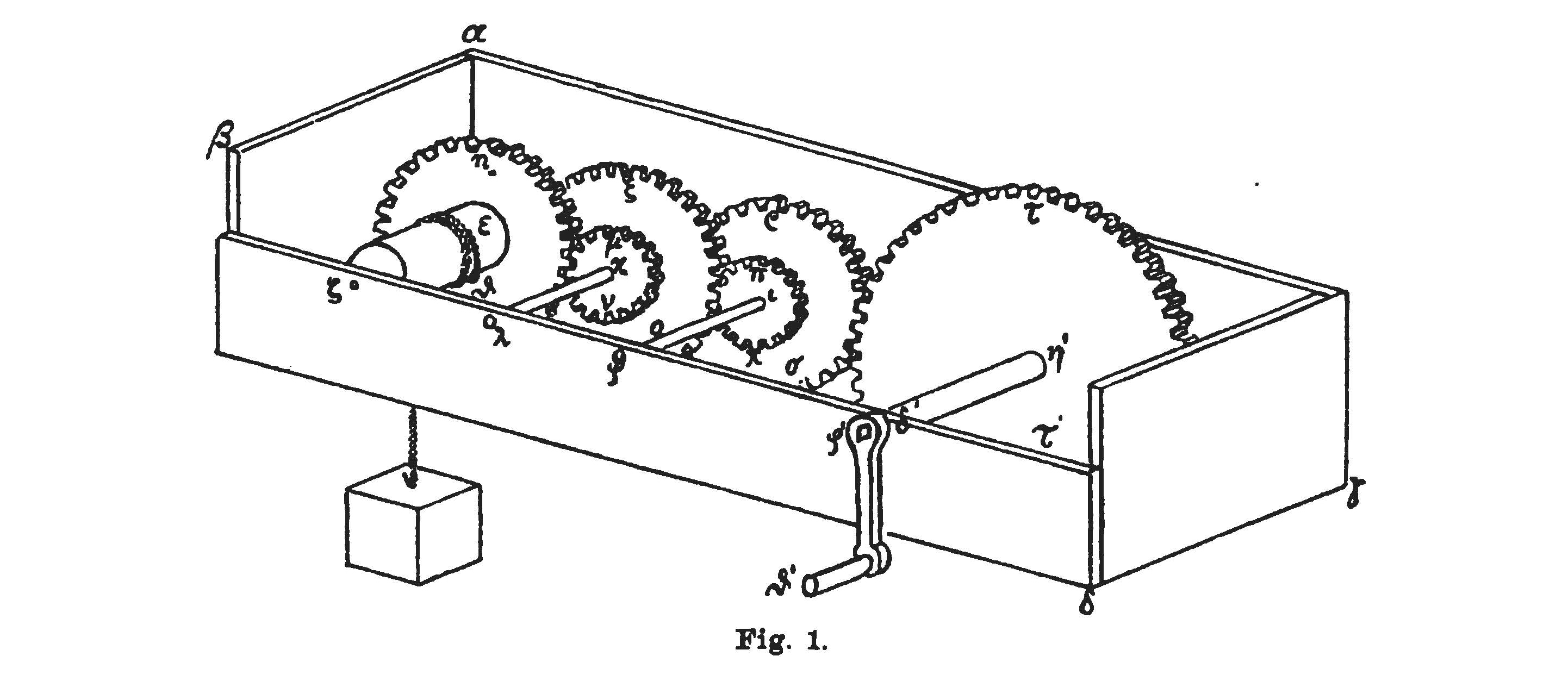 Abbildung 4: Heron, „Mechanica“, Opera quae supersunt omnia, Bd. II.I, hrsg. von L. Nix und W. Schmidt, S. 2 (Detail).
Abbildung 4: Heron, „Mechanica“, Opera quae supersunt omnia, Bd. II.I, hrsg. von L. Nix und W. Schmidt, S. 2 (Detail).
Damit scheint das Rätsel gelöst: Leibniz könnte die Schilderung der „Baroulkos-Maschine“ in Herons Mechanica mit Perraults Beschreibung der eigenen Hebemaschine verwechselt haben, was auch deshalb wahrscheinlich ist, da beide die gleiche Funktion erfüllten und letztlich auf einer ähnlichen Grundmaschine beruhten (nämlich der Hebewinde). So einfach die Lösung? Wohl kaum. Denn der griechische Urtext von Herons Mechanica hat den Zusammenbruch der antiken Zivilisation nicht überlebt. Erhalten ist lediglich eine arabische Übersetzung aus dem 9. Jh., von der zu Leibnizʼ Zeit – wie Hans van de Velde gezeigt hat – nur eine in Leiden aufbewahrte Handschrift aus dem 13. Jh. bekannt war. Wir wissen nicht, ob Leibniz von der Existenz dieser Handschrift wusste. Er konnte aber ohnehin kein Arabisch und zu seiner Zeit war keine zugängliche Übersetzung verfügbar. Noch ein Jahrhundert später plante Friedrich der Große – vergeblich – die Leidener Handschrift ins Lateinische oder Französische übertragen zu lassen. Herons Abhandlung kann daher nicht die Quelle gewesen sein, von der Leibniz seine Kenntnis der Baroulkos-Maschine geschöpft hat. Unser Rätsel hält noch immer stand.
Wenn demnach die direkte Überlieferung auszuschließen ist, muss die indirekte Überlieferung in den Blick genommen werden. Es stellt sich also die Frage: Gab es zu Leibnizʼ Zeit eine alternative Quelle, aus der frühneuzeitliche Gelehrte von Herons „Baroulkos-Maschine“ erfahren konnten? Ja, die gab es: den spätantiken Mathematiker Pappos von Alexandria (4.Jh.n.Chr.). Im achten Buch seiner auf Griechisch verfassten und in der Frühneuzeit intensiv studierten „mathematischen Sammlungen“ finden sich explizite Hinweise auf (bzw. Auszüge aus) Herons Mechanica – meistens als „Baroulkos“ (βαρουλκός) bezeichnet. Zudem enthält Papposʼ Schrift die Beschreibung einer Maschine, die mit der in der arabischen Überlieferung von Herons Text dargestellten Hebewinde übereinstimmt (Mathematicae collectiones VIII 6, 10). Damit sind wir sehr wahrscheinlich der von Leibniz so bezeichneten „Baroulkos-Maschine“ auf die Spur gekommen.
Papposʼ Collectiones konnte man zu Leibnizʼ Zeit in der humanistischen Latinisierung von Federico Commandino lesen, welche wenige Jahre vor Leibnizʼ Pariser Aufenthalt neu gedruckt worden war. Die Seiten aus der zweiten Ausgabe (1660) der Commandino-Übersetzung, auf denen die „Baroulkos-Maschine“ beschrieben und mit einer Zeichnung dargestellt wird, sind teilweise in beiden folgenden Abbildungen wiedergegeben:

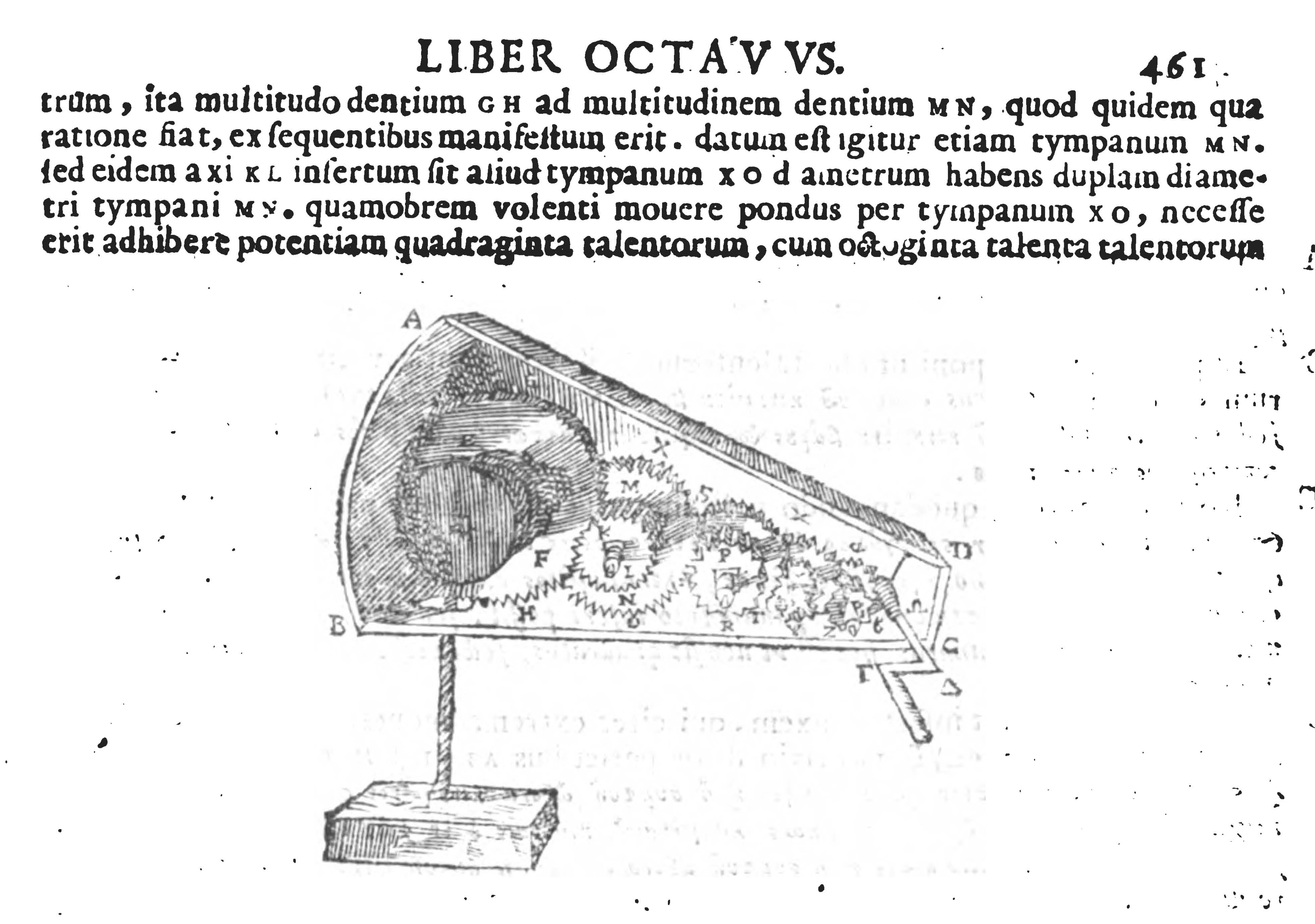 Abbildung 5 und 6: Pappos, Mathematicae collectiones, Venedig 1660, S. 460-461, Details.
Abbildung 5 und 6: Pappos, Mathematicae collectiones, Venedig 1660, S. 460-461, Details.
Leibniz hatte also bei Pappos – in einer bequemen und eleganten lateinischen Textfassung – von der Hebewinde lesen können, die er in seinen Ausführungen über die Reibung aus dem Jahr 1675 irrtümlich Perrault zuschrieb. Man kann mit einer gewissen Wahrscheinlichkeit auch erklären, wie Leibniz auf die Stelle bei Pappos aufmerksam geworden ist. Etwa zur gleichen Zeit, als er seine ersten Überlegungen über die Reibung verfasste, setzte er sich weitgehend mit der Abhandlung Mechanica sive De motu des englischen Mathematikers John Wallis (1616-1703) auseinander. (Umfangreiche handschriftliche Auszüge daraus werden derzeit im Band VIII.2 der Leibniz-Edition zum ersten Mal veröffentlicht.) Im dritten Teil dieser Abhandlung, der mit den traditionellen fünf „Grundmaschinen“ (Hebel, Keil, Flaschenzug, Rad auf Welle, Schraube) befasst ist, verweist Wallis auf Papposʼ Referat über Herons „Baroulkos“ (worunter Wallis, ein guter Kenner von Pappos, zu Recht nicht Herons Maschine, sondern Herons Buch verstand). Es ist daher plausibel, dass Leibniz von seiner Wallis-Lektüre den Anstoß empfang, sich Papposʼ Referat genauer anzuschauen. Und dies dürfte in demselben zeitlichen und gedanklichen Zusammenhang geschehen sein, in dem Leibniz auch seine eigenen Überlegungen über das Phänomen der Reibung entwickelte.
 Abbildung 7: Bayerische Staatsbibliothek München, 10408787 4 Math.a. 319, S. 617, urn:nbn:de:bvb:12-bsb10053170-1.
Abbildung 7: Bayerische Staatsbibliothek München, 10408787 4 Math.a. 319, S. 617, urn:nbn:de:bvb:12-bsb10053170-1.
Wenn diese Vermutung zutrifft, dann ist auch die Verwechselung, die Leibniz bei der Zuschreibung der Urheberschaft der „Baroulkos-Maschine“ unterlaufen ist, nicht überraschend. Hauptsächlich eine Eigenschaft dieser Maschine war Leibniz aus den Quellen im Gedächtnis hängen geblieben, nämlich dass durch geschickte technische Anwendungen reibungsbedingter Kraftverbrauch entscheidend verringert werden kann. Eben diese Eigenschaft hatte Perrault an dem von ihm entworfenen Kran angepriesen. Beide Maschinen sind in Leibnizʼ Gedächtnis offenbar zu einer einzigen verschmolzen. Freilich ein Missverständnis, aber ein kreatives. Die verschlungenen Wege der Quellenrezeption in der Geistesgeschichte verlangen nicht selten detektivischen Spürsinn und führen oft zu überraschenden Ergebnissen.
Autor: Paolo Rubini, wissenschaftlicher Mitarbeiter der Leibniz-Editionsstelle Berlin, BBAW.
Literaturverzeichnis
Galilei, G., Discorsi e dimostrazioni matematiche intorno a due nuove scienze attinenti alla mecanica e i movimenti locali, Leiden 1638
Heron von Alexandrien, Opera quae supersunt omnia, Bd. II.1: Mechanica et catoptrica, hrsg. von L. Nix und W. Schmidt, Leipzig 1900.
LSB VIII.2: Leibnizʼ Schriften und Briefe, hrsg. von der Berlin-Brandenburgischen Akademie der Wissenschaften, Bd. VIII.2, erscheint 2016.
Leibniz, G. W., Aus und zu John Wallis, Mechanica sive De motu, in LSB VIII.2, N.~8.
Leibniz, G. W., Du frottement. Essais géometriques en fait de mécanique. Zweite Fassung, in LSB VIII.2, N.~362. Handschriftliche Quelle: Hannover, Gottfried-Wilhelm-Leibniz-Bibliothek, LH XXXV 9, 11 Bl.~3-4.
Nohl, H., Index Vitruvianus, Leipzig 1876.
Pappos von Alexandrien, Collectionis quae supersunt e libris manu scriptis, hrsg. von F. Hultsch, Bd. III.1, Berlin 1678.
Pappos von Alexandrien, Mathematicae collectiones, a Federico Commadino in Latinum conversae et commentariis illustratae, Venedig 1589; 2. Ausgabe, Venedig 1660.
van de Velde, H., „From Qusṭā b. Lūqā to Carra de Vaux. On the History of the Edition and Translation of the Barulcus, also called ʼMechanicʼ, by Heron of Alexandria“, Journal of Islamic Manuscripts 1 (2010), S.~95-100.
Vitruvius, De architectura libri decem, hrsg. von V. Rose und H. Müller-Strübing, Leipzig 1867; 2. Ausgabe, hrsg. von V. Rose, Leipzig 1899.
Vitruvius, De architectura libri decem, hrsg. von F. Krohn, Leipzig 1912.
Vitruvius, Les dix livres dʼarchitecture, corrigez et traduits nouvellement en François, avec des Notes et des Figures, [hrsg. von C. Perrault], Paris 1673.
Wallis, J., Mechanica sive de motu tractatus geometricus, 2 Bde., London 1670-1671.
Online-Projekt „Leibniz-Objekt des Monats“:
Das Projekt „Leibniz-Objekt des Monats“ stellt mit Expertenbeiträgen über das Leibniz-Jahr 2016 hinweg jeden Monat ein Archivale oder eine Handschrift vor. Ziel ist es, einerseits die grundlegende Bedeutung von Leibniz für die Akademiegeschichte herauszustellen und andererseits die Arbeit „an Leibniz“ sichtbar zu machen, die tagtäglich an der Akademie stattfindet. Die gezeigten „Objekte“ zeichnen in ihrer Gesamtheit ein ganz eigenes Bild vom Leben und Wirken des großen Visionärs.



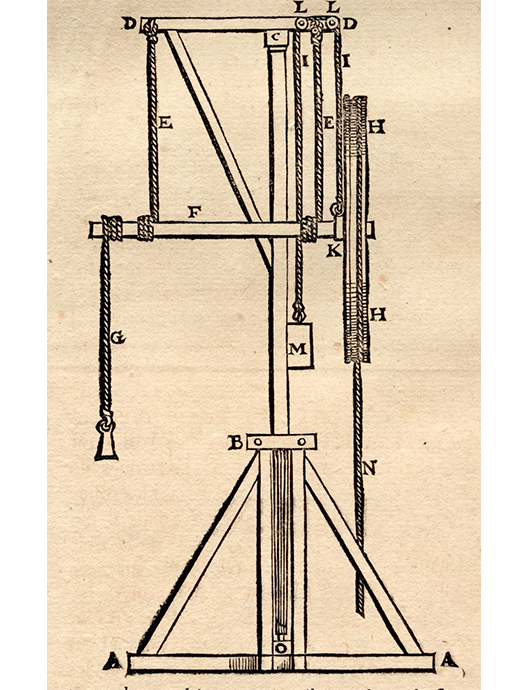
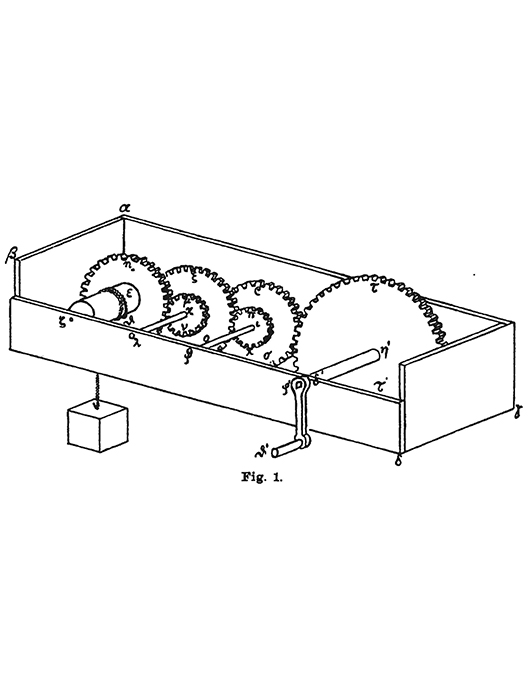
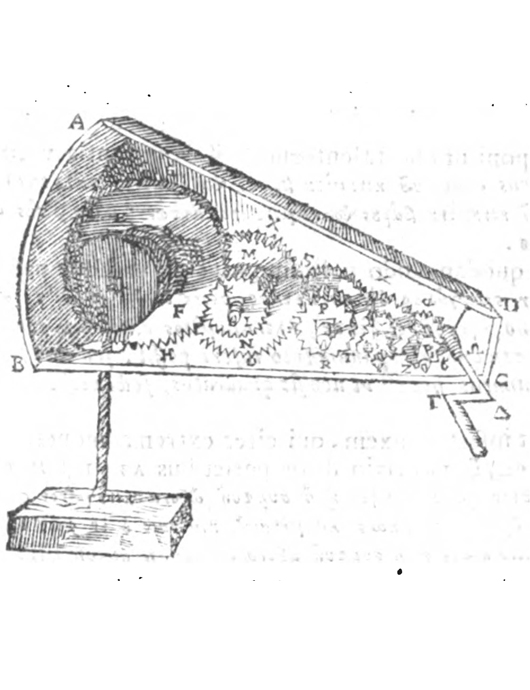

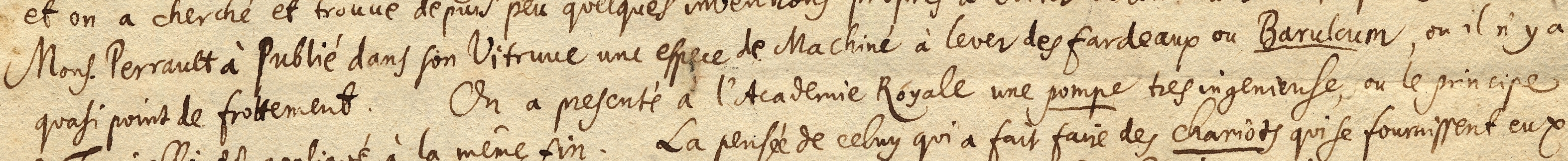

 Abbildung 4: Heron, „Mechanica“, Opera quae supersunt omnia
Abbildung 4: Heron, „Mechanica“, Opera quae supersunt omnia

