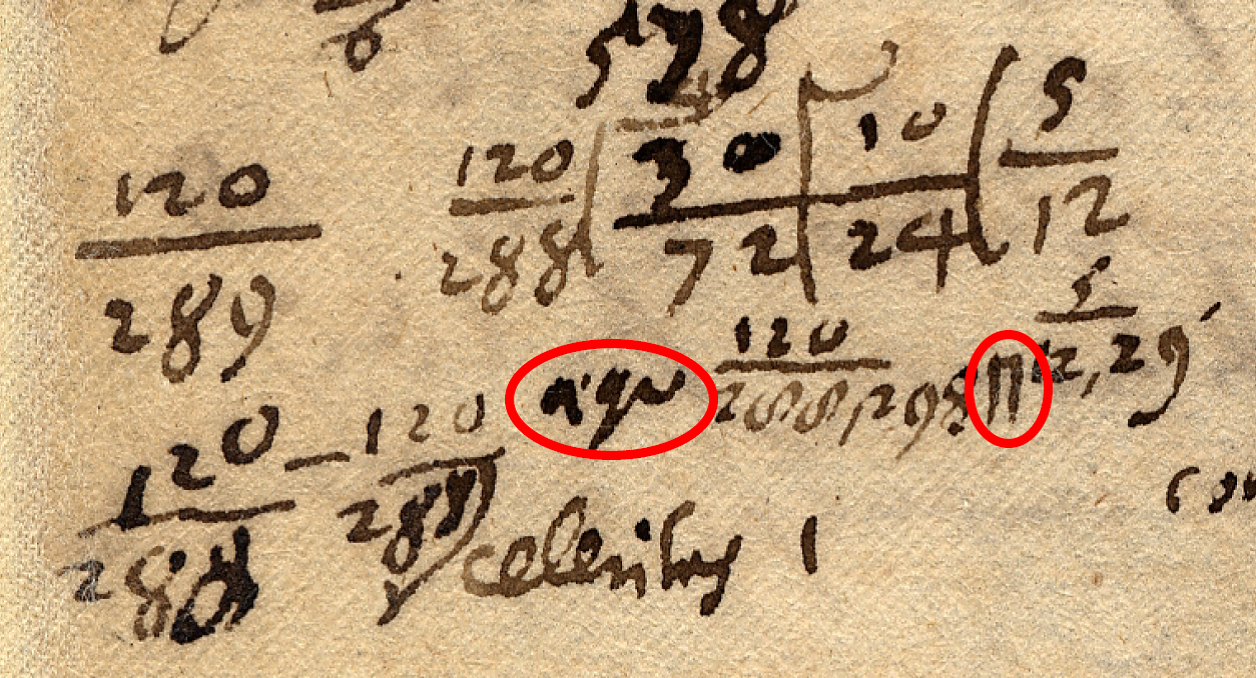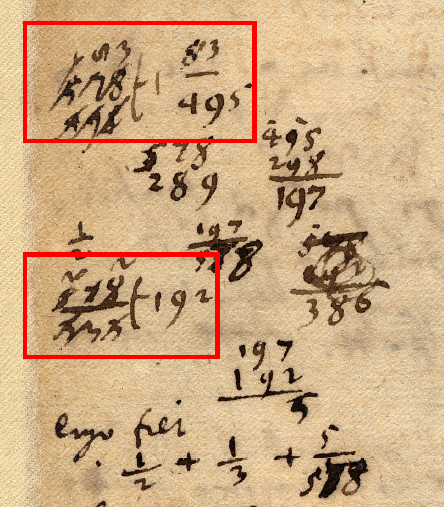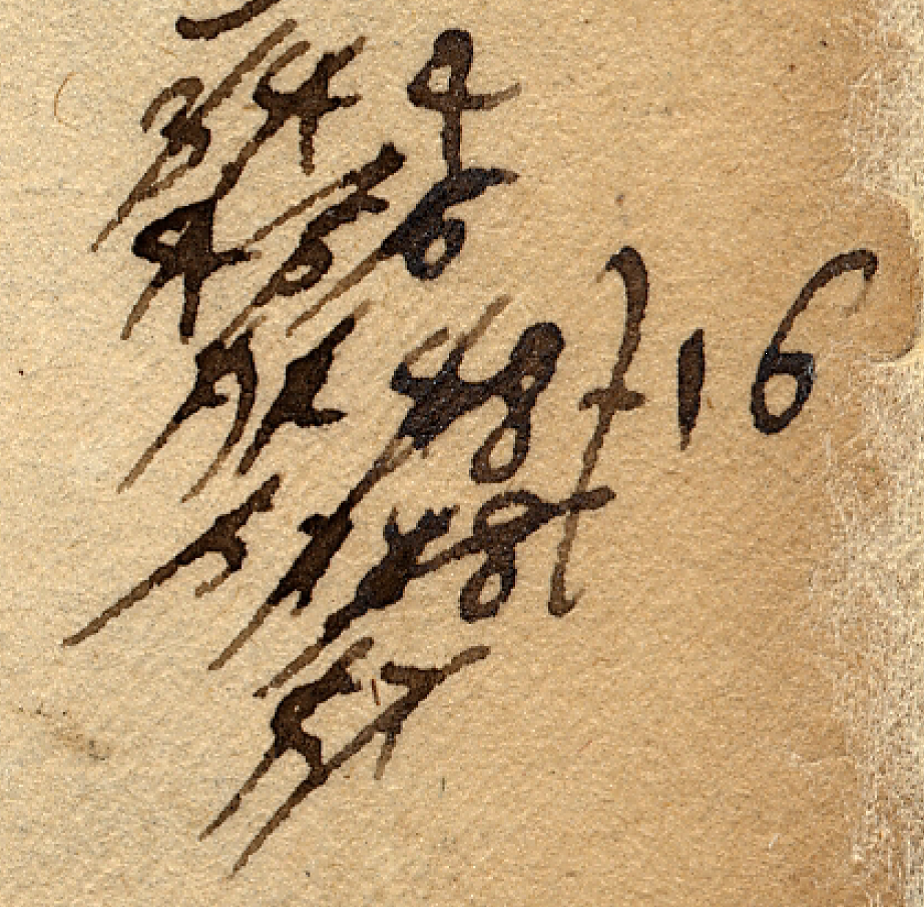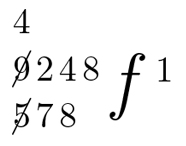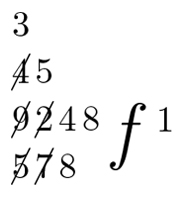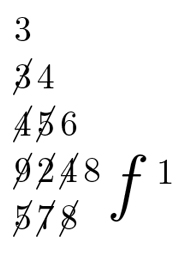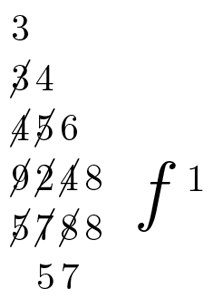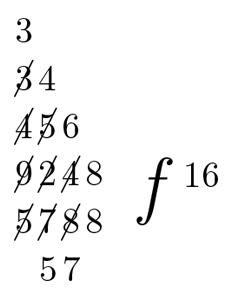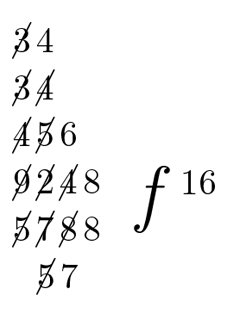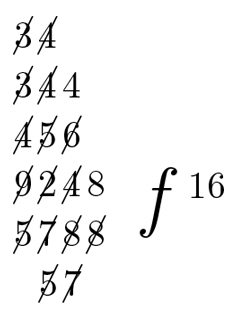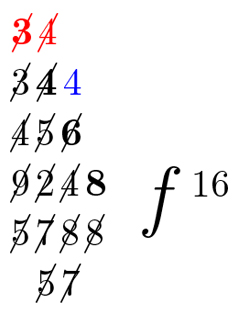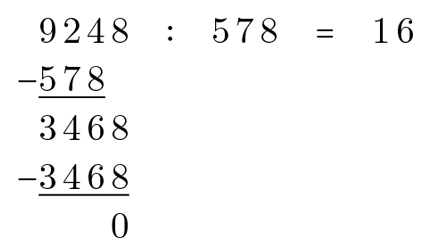Leibniz-Objekt des Monats
Oktober 2016: Rechnen wie Leibniz - Die Überwärtsdivision
Abbildungen im Slider: Die Scheda secundo-sexta (6-2) aus Leibnizens Untersuchungen zum Stoß (De corporum concursu, LH XXXV 9, 23 Bl. 15-20, LH XXXVII 5 Bl. 91). In der Reihe VIII der Akademie-Ausgabe werden diese Untersuchungen im dritten Band ediert, der gerade in Bearbeitung ist: http://leibniz-berlin.bbaw.de/leibniz-online.
Rechnen wie Leibniz - Die Überwärtsdivision
Im Zuge seiner intensiven Auseinandersetzung mit den Stoßgesetzen im Januar 1678 gewinnt Leibniz die für uns heute selbstverständliche Erkenntnis, dass bei der Bewegung von Körpern Kräfte wirken. Leibniz wird hierfür später den Begriff Dynamik in die Welt setzen, der heute ein Teilgebiet der Mechanik bezeichnet und genauso wenig aus der Physik wie aus unserer Vorstellung wegzudenken ist.
Dass die Phänomene, die sich beim Zusammenstoß von Körpern zeigen, anders nicht zu erklären sind, fand Leibniz erst heraus, nachdem er frühere Annahmen in Frage gestellt und schließlich verworfen hatte. Dieses Ringen schlug sich auf den Blättern von zehn Bögen bzw. Heften (schedae) nieder, die uns Leibniz gut geordnet und beschriftet in seinem Nachlass überliefert hat. Ein entscheidender Moment ereignet sich im zweiten Teil des sechsten Bogens, als Leibniz seine Berechnungsformeln mit Werten füttert, die aus Experimenten stammen.

Abbildung: Die erste Seite der Scheda secundo-sexta (LH XXXV 9, 23 Bl. 15r) aus Leibnizens Untersuchungen zum Stoß (De corporum concursu, LH XXXV 9, 23 Bl. 15-20, LH XXXVII 5 Bl. 91). In der Reihe VIII der Akademie-Ausgabe werden diese Untersuchungen im dritten Band ediert, der gerade in Bearbeitung ist: http://leibniz-berlin.bbaw.de/leibniz-online.
Mathematische Notationen
Richten wir den Blick auf die vielen Gleichungen, Rechnungen, Zahlentabellen auf diesen Blättern der Scheda 6-2, dann stoßen wir auf Zeichen, die heute nicht mehr gebräuchlich sind. Anders als das Integralzeichen (∫), das wir Leibniz verdanken, hat sich keines seiner Doppelvorzeichen (signa ambigua) durchsetzen können, für die er insgesamt sechs Systeme schuf:

Abbildung: Die +/- Doppelvorzeichen sind jeweils von oben nach unten zu lesen, hier also minusplus, plusminus, plusminus. Die zwei kleinen Bögen in der Zeile darüber sind Zeichen für die Multiplikation (um 180° gedreht werden sie zu einem Zeichen für die Division).
Um die Gleichheit auszudrücken, kennt Leibniz mehrere Zeichen, darunter auch unser heutiges. Manchmal schreibt er dafür aequ. bzw. aeq. (für aequalis) oder benutzt ein Zeichen, das symbolisch eine Waage darstellt:
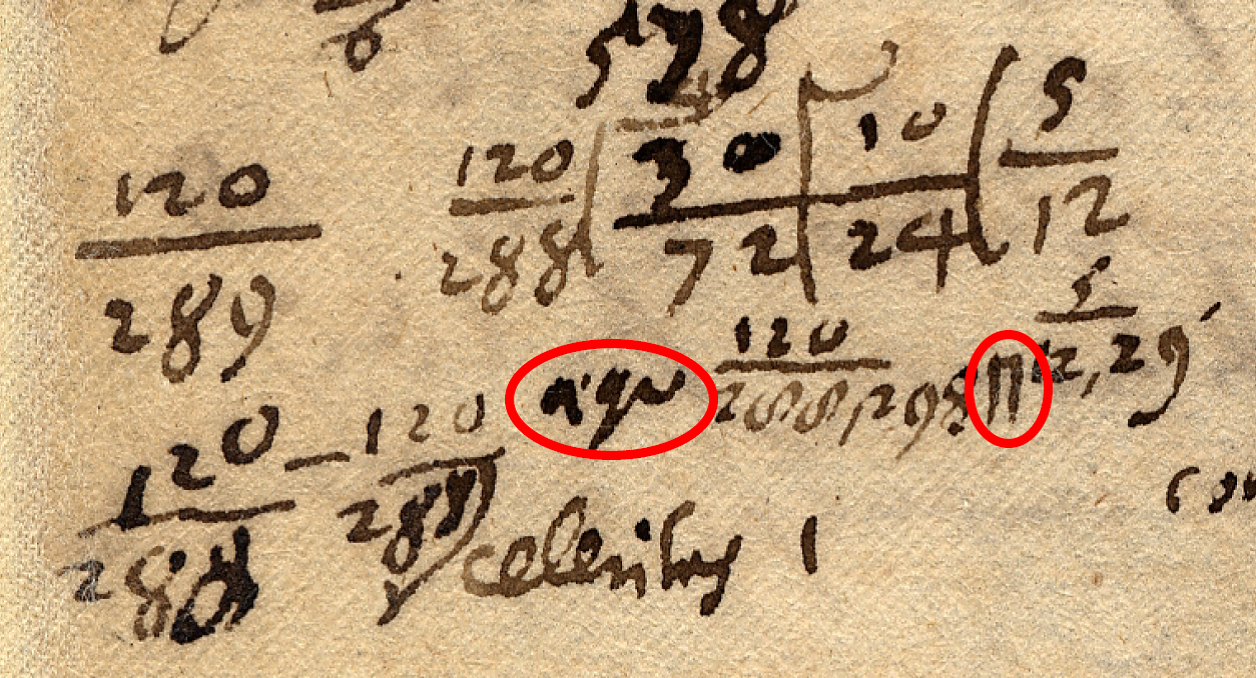
Abbildung: Zwei Schreibungen, mit denen Leibniz die Gleichheit ausdrückt: Die Abkürzung aequ. und ein eigenes Zeichen.
Überwärtsdivision
Aber auch die Rechnungen auf den Blättern der Scheda 6-2 erschließen sich uns nicht mehr auf Anhieb. So benutzt Leibniz für die schriftliche Division ein Rechenverfahren, das durch unsere heutige Art zu dividieren völlig in Vergessenheit geraten ist. Die von Leibniz verwendete Überwärtsdivision verschwindet im Laufe des 19. Jahrhunderts vollständig; das letzte Lehrbuch, das Dividieren allein auf diese Weise erklärte, dürfte die Rechenkunst von Johann Baptist Lechner aus dem Jahr 1800 sein. Kein Wunder also, dass sich durch einfaches Googeln nicht mehr herausfinden lässt, wie dieses Rechenverfahren funktioniert.
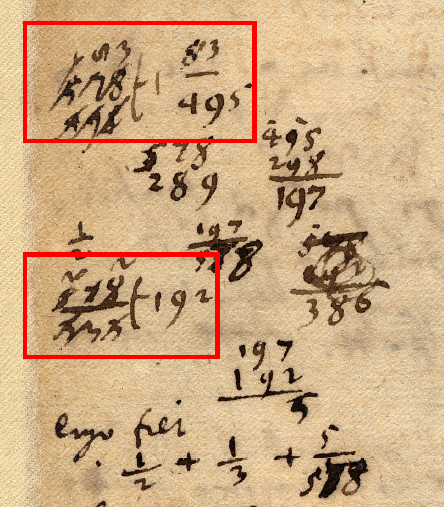

Abbildung: Zum Dividieren verwendete Leibniz ein heute vergessenes Verfahren, die Überwärtsdivision.
Das Ergebnis seiner Division weist Leibniz mit einem stilisierten f aus, das facit (es macht) bedeutet. So lesen wir zumindest deutlich, kurz bevor das Papier am Rand abbricht, dass die Rechnung, die Leibniz hier durchführt, 16 ergibt. Aber wo stehen Dividend und Divisor bei dieser Art der Division?
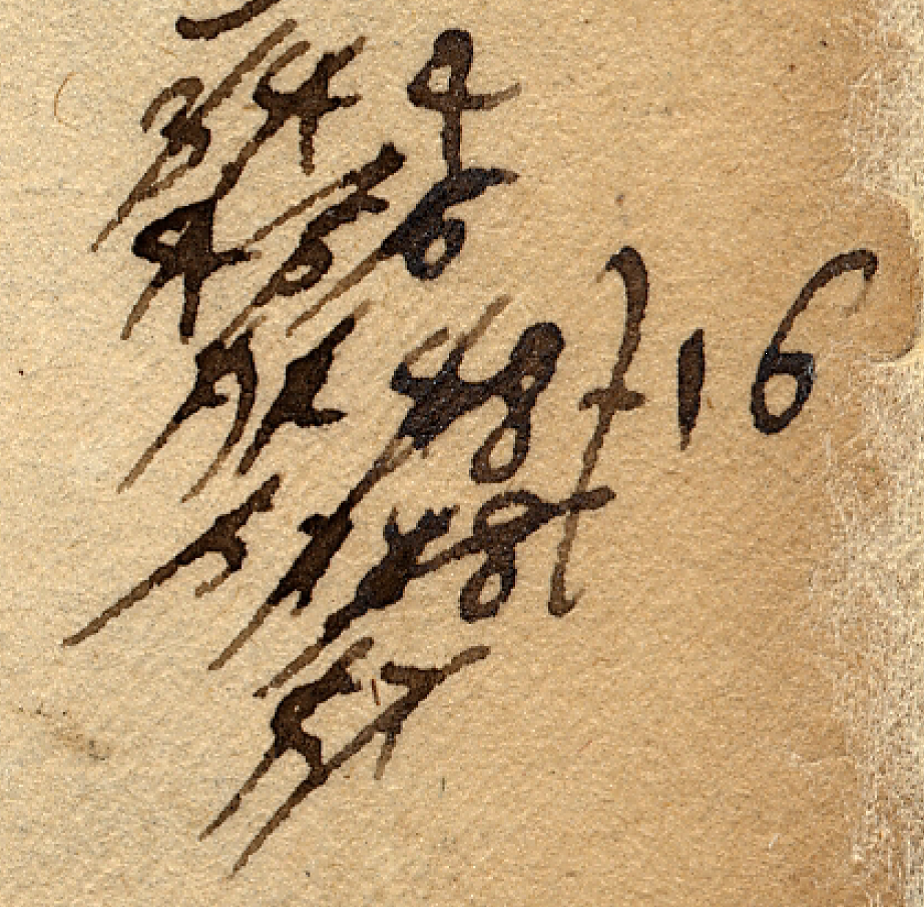
Abbildung: Eine Überwärtsdivision: Streichungen und Zahlenanordnung sind charakteristisch für dieses Rechenverfahren.
Tatsächlich gehen Dividend und Divisor in den vielen Ziffern unter, die im Zuge der Rechenschritte mit angeschrieben und wieder gestrichen werden. Dass Leibniz an diesen Stellen der Handschrift überhaupt eine Division durchführt, kommt einem daher gar nicht in den Sinn. In moderner Notation lautet die hier von Leibniz durchgeführte Rechnung:
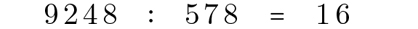
Beim schriftlichen Dividieren haben wir gelernt, den Divisor neben den Dividenden zu schreiben und alle Schritte mitsamt den Zwischenergebnissen darunter (also unterwärts) aufzuführen. Bei der Überwärtsdivision verhält es sich genau umgekehrt. Dividend und Divisor stehen mit ihren jeweils höchsten Stellen linksbündig übereinander:
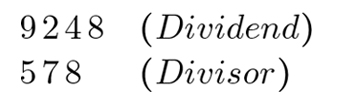
In einem ersten Schritt ist zu bestimmen, wie oft 578 in 924 enthalten ist. Dieser Wert des Quotienten ist hier ohne langes Ausprobieren schnell gefunden und wird rechts notiert:
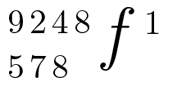
Nun wird die erste Stelle des Divisors (ohne Rücksicht auf den Stellenwert) mit dem Wert des Quotienten multipliziert. Das Ergebnis dieser Multiplikation wird danach von dem Zahlenwert der ersten Dividendenstelle (die genau darüber steht) subtrahiert. Die Differenz (9-5) ergibt den Wert 4, der an derselben Stelle über dem Dividenden zu notieren ist. Die Stellen des Dividenden und Divisors, die bei diesen Operationen benutzt worden sind, werden quer, wie in der Handschrift zu sehen, durchgestrichen:
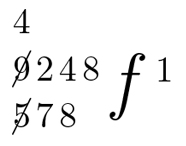
Anschließend ist mit der zweiten Stelle des Divisors fortzufahren. Das Produkt 7 wird von der darüber stehenden Zahl 42 subtrahiert, die sich aus zwei Stellen zusammensetzt (aus der Differenz der vorangegangenen Subtraktion und aus der zweiten Stelle des Dividenden). Die Differenz von 42 minus 7 ergibt den Wert 35, der über den Minuenden so zu schreiben ist, dass keine Lücke bleibt; die verwendeten Zahlen sind wieder zu streichen:
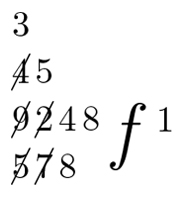
Zum Abschluss dieses ersten Rechenschritts wird 8 von 354 subtrahiert, was 346 ergibt und wie folgt über den Minuenden zu notieren ist, der seinerseits zusammen mit der 8 des Divisors durchgestrichen wird:
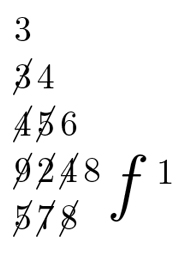
Nach Abschluss dieses ersten Rechenschritts, wird der Divisor um eine Stelle nach rechts verschoben und so unter den Dividenden geschrieben, dass keine Lücke bleibt:
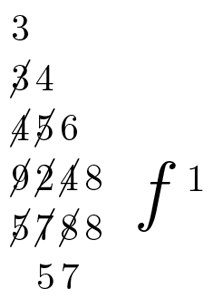
Wie oft ist 578 in 3468 enthalten? Diese Größenordnung scheint fast eine eigene Rechnung zu erfordern. Aber es genügt den Faktor abzuschätzen: 7 ist sicherlich zu viel, 6 der Wert, mit dem sich weiterrechnen lässt:
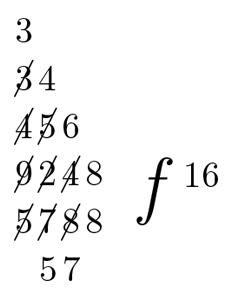
Mit 6 wird nun der Zahlenwert der ersten Divisorstelle (5) multipliziert und das Ergebnis von der Zahl subtrahiert, die sich aus den ungestrichenen Stellen darüber und links davon ergibt. Wir rechnen also 34 minus 30. Der Rest wird darüber notiert:
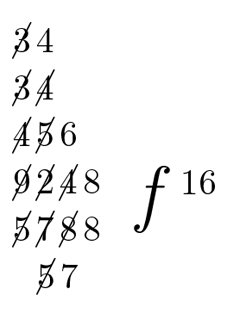
Mit der zweiten Divisorstelle erhalten wir den Wert (7x6=) 42, der von der darüberstehenden Zahl (46) substrahiert wird. Das Ergebnis ist wieder überwärts festzuhalten:
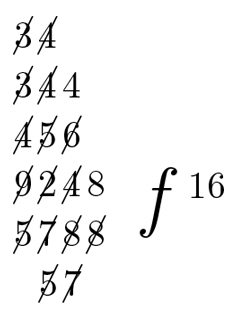
Aus der letzten Divisorstelle erhält man den Wert (8x6=) 48. Dieselbe Zahl liefern auch die darüberstehenden noch nicht gestrichenen Ziffern, so dass die Subtraktion Null ergibt und die Division ohne Rest aufgeht.
In der handschriftlichen Fassung der Überwärtsdivision fehlen die hier im Folgenden rot markierten Ziffern der obersten Zeile, die Leibniz offenbar im Kopf behalten hat:
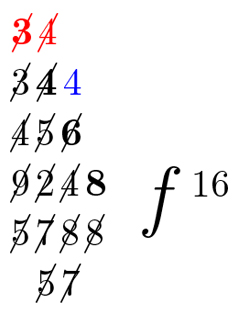
Da er aber auch die letzte Divisorstelle ausstreicht und auch den vorangegangenen Rest 4 notiert (hier blau), hat er mit dem Verfahren offenbar bis zum Schluss weitergerechnet. Dass die Zahl 3468 (hier fett), die er bereits nach dem ersten Schritt erhält, ohne Rest durch 6 teilbar ist, hat er vielleicht nicht gesehen oder erst noch überprüfen wollen.
Überwärts oder unterwärts dividieren?
Die Überwärtsdivision unterscheidet sich nicht von unserem heutigen Rechenverfahren, was die einzelnen Operationen angeht. Um die schriftliche Division unterwärts auszuführen ist es genauso nötig, das richtige Vielfache abzuschätzen, zu multiplizieren und zu subtrahieren. Unterwärts ausgeführt sieht die schriftliche Division für unseren Fall wie folgt aus:
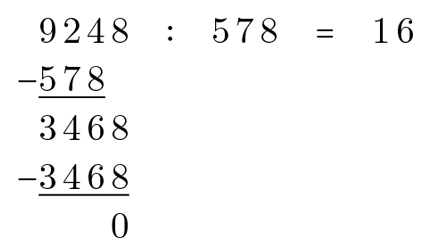
In beiden Rechenverfahren ist es reine Kopfsache, den passenden Zahlenwert für den Quotienten durch Ausprobieren herauszufinden. Dagegen geht die Multiplikation bei der Überwärtsdivision leichter von der Hand, weil immer nur jeweils eine Stelle des Divisors mit dem Quotienten mal genommen wird und somit keine Überträge entstehen. Bei unserer Unterwärtsdivision ist dies anders: Hier wird der gesamte mehrstellige Divisor mit dem Quotienten multipliziert, was aber schriftlich erfolgen kann. Gleiches gilt für die Subtraktion: Bei der Überwärtsdivision muss sie im Kopf geleistet werden, während sie sich in der Unterwärtsdivision schriftlich durchführen lässt. Verglichen mit der Überwärtsdivision scheint unser heutiges Verfahren daher nicht unbedingt einfacher zu sein, sondern vor allem sicherer. Denn sowohl die Multiplikation als auch die Subtraktion können darin schriftlich ausgeführt werden. Wer die Subtraktion im Kopf aber nicht scheut, fährt mit dem von Leibniz verwendeten Verfahren womöglich genauso gut oder besser. Probieren Sie es aus!
Autor: Harald Siebert, Leibniz-Edition Berlin der Berlin-Brandenburgischen Akademie der Wissenschaften
Literatur:
Fichant, Michel: La réforme de la dynamique, Paris : Vrin, 1994.
Tropfke, Johannes: Geschichte der Elementarmathematik, Bd 1, vollst. neu bearb. v. Kurt Vogel, Karin Reich, Helmuth Gericke, 4. Auf., Berlin u. New York: De Gruyter, 1980.
Trunk, Achim: „Sechs Systeme: Leibniz und seine signa ambigua“, in: Wenchao Li, „Für unser Glück oder das Glück anderer“. Vorträge des X. Internationalen Leibniz-Kongresses. Hannover, 18.-23. Juli 2016, 5 Bde, Hildesheim u.a.: Georg Olms, 2016, Bd 4, S. 191-207.
Online-Projekt „Leibniz-Objekt des Monats“:
Das Projekt „Leibniz-Objekt des Monats“ stellt mit Expertenbeiträgen über das Leibniz-Jahr 2016 hinweg jeden Monat ein Archivale oder eine Handschrift vor. Ziel ist es, einerseits die grundlegende Bedeutung von Leibniz für die Akademiegeschichte herauszustellen und andererseits die Arbeit „an Leibniz“ sichtbar zu machen, die tagtäglich an der Akademie stattfindet. Die gezeigten „Objekte“ zeichnen in ihrer Gesamtheit ein ganz eigenes Bild vom Leben und Wirken des großen Visionärs.